Solve Sudoku Puzzle with Z3 Theorem Prover

Today I will explain Z3 Theorem Prover, a sophisticated theorem prover developed by Microsoft Research. Renowned for its efficacy in software verification and complex problem-solving, Z3 stands out for its accurate solutions and efficient problem-solving algorithms.

What is Z3 Theorem Prover?

A theorem prover is a software tool that verifies mathematical theorems using computational algorithms, ensuring their correctness through formal proof techniques and logical analysis. Consider a case with two integer variables, x and y. The goal is to determine values for x and y that satisfy the conditions x > 2, y < 10, and x + 2\*y == 7. To solve this, a theorem prover like Z3 can be used, which is adept at finding solutions to such constraints.

Installing Z3 Python

pip install z3-solver

from z3 import Int, solve

x = Int("x")
y = Int("y")

solution = solve(x > 2, y < 10, x + 2 \* y == 7)
print(solution) # prints [x = 3, y = 2]

Pretty cool, right? Z3 is able to find a solution that satisfies the above constraints. Let's take a look at a more complex problem, solving a Sudoku puzzle.

Solving a Sudoku Puzzle with Z3

For simplicity, we'll use a 9x9 Sudoku puzzle as an example. A Sudoku puzzle consists of a 9x9 grid, with each cell containing a number from 1 to 9. The puzzle's objective is to fill in the grid so that each row, column, and 3x3 subgrid contains the numbers 1 through 9 exactly once. The puzzle begins with some cells already filled in, and the task is to fill in the remaining cells.

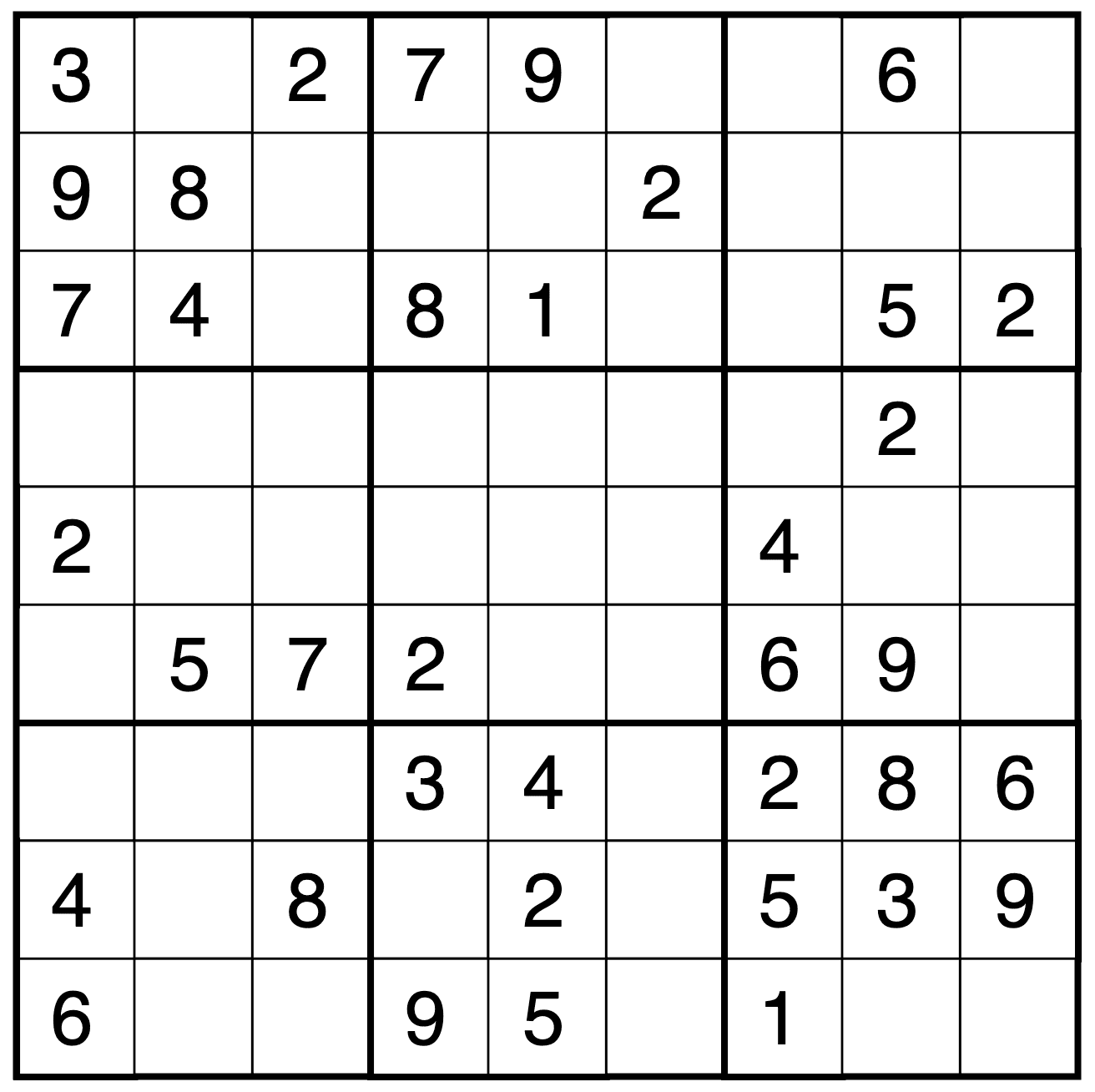
Defining Constraints in Sudoku

To solve this using Z3, we need to define the constraints of the puzzle. The constraints are as follows:

Grid Constraint: Each cell must be between 1 and 9.
Row Constraint: Each row must contain distinct numbers from 1 to 9.
Column Constraint: Each column must also have distinct numbers from 1 to 9.
Subgrid Constraint: Each 3x3 subgrid must have distinct numbers from 1 to 9.

Representing the constraints in Z3

# Create a 9x9 matrix of integer variables
sudoku_grid = [[Int(f"cell*{row}\_{col}") for col in range(9)]
               for row in range(9)]

# Constraint 1: Each cell must be between 1 and 9
cell_constraints = [
    And(1 <= cell, cell <= 9)
    for row in sudoku_grid
    for cell in row
]

# Constraint 2: Each row must have distinct values
row_constraints = [Distinct(row) for row in sudoku_grid]

# Constraint 3: Each column must have distinct values
col_constraints = [
    Distinct([sudoku_grid[row][col] for row in range(9)])
    for col in range(9)
]

# Constraint 4: Each 3x3 subgrid must have distinct values
subgrid_constraints = [
    Distinct([
        sudoku_grid[3 * block_row + row][3 * block_col + col]
        for row in range(3)
        for col in range(3)
    ])
    for block_row in range(3)
    for block_col in range(3)
]

# Combine all constraints
all_constraints = cell_constraints + row_constraints + col_constraints + subgrid_constraints

Executing the constraints in Z3

# Create a Sudoku puzzle. 0 represents an empty cell
sudoku_puzzle = [
    [3, 0, 2, 7, 9, 0, 0, 6, 0],
    [9, 8, 0, 0, 0, 2, 0, 0, 0],
    [7, 4, 0, 8, 1, 0, 0, 5, 2],
    [0, 0, 0, 0, 0, 0, 0, 2, 0],
    [2, 0, 0, 0, 0, 0, 4, 0, 0],
    [0, 5, 7, 2, 0, 0, 6, 9, 0],
    [0, 0, 0, 3, 4, 0, 2, 8, 6],
    [4, 0, 8, 0, 2, 0, 5, 3, 9],
    [6, 0, 0, 9, 5, 0, 1, 0, 0],
]

# Add constraints for the given Sudoku puzzle
puzzle_constraints = [
    If(
        sudoku_puzzle[row][col] == 0,
        True,
        sudoku_grid[row][col] == sudoku_puzzle[row][col],
    )
    for row in range(9)
    for col in range(9)
]

solver = Solver()
solver.add(all_constraints + puzzle_constraints)

# Solve the Sudoku puzzle and print the solution if available
if solver.check() == sat:
    model = solver.model()
    solution = [
        [model.evaluate(sudoku_grid[row][col]) for col in range(9)] for row in range(9)
    ]
    print(solution)
else:
    print("Failed to solve")

When we run the above code, we get the following solution:

[[3, 1, 2, 7, 9, 5, 8, 6, 4],
 [9, 8, 5, 4, 6, 2, 3, 1, 7],
 [7, 4, 6, 8, 1, 3, 9, 5, 2],
 [1, 6, 9, 5, 3, 8, 7, 2, 4],
 [2, 3, 1, 6, 7, 9, 4, 0, 0],
 [8, 5, 7, 2, 4, 1, 6, 9, 3],
 [5, 9, 0, 3, 4, 7, 2, 8, 6],
 [4, 7, 8, 1, 2, 6, 5, 3, 9],
 [6, 2, 3, 9, 5, 4, 1, 7, 8]]

Z3 Applications

Z3 has numerous exciting applications. My personal favorite is Symbolic Execution. Symbolic Execution leverages the power of Z3 for software verification. It is utilized to detect bugs in software by exploring all possible paths through the program. This technique is incredibly powerful for identifying bugs in complex software.